本系列文章致力于对近期笔者关于反常、瞬子、扩展场构型以及QCD的U(1)问题、强CP问题等相关内容做一个简单的复习回顾,以便梳理思路。
本文首先给出一个关于反常的快速回顾。
主要参考:The Quantum Theory of Fields, Vol.II, Chapter 22, Steven Weinberg
一句话来说,反常就是经典的对称性在量子化过程中被破坏了。从历史上来说,对反常最早期的探索来源于对 $\pi_0\rightarrow\gamma\gamma$ 衰变速率的研究。从 QCD 的有效理论中,我们知道在上下夸克的零质量近似下,手征有效场论有一个整体的 $SU(2)_{L}\times{SU(2)_R}$ 的手征对称性,并且 $\pi$ 介子可以作为这个对称性自发破缺的 Goldstone 玻色子1。当电磁相互作用介入其中时,这个 $SU(2)\times SU(2)$ 对称性的绝大部分都被显著地破坏了,因为显然电磁场会与其中非电中性的生成元(部分对应于一些 Goldstone 粒子)产生相互作用。然而,一个合理的猜测是, $SU(2)\times SU(2)$ 对称性中那些电中性生成元对应的 $U(1)_L\times U(1)_R$ 子群(更常用地,我们会写成等价的 $U(1)_V\times U(1)_A$,即矢量与轴矢量 $U(1)$ 对称性)至少应当被保留下来。
但是,这个想法却在实验上遇到了困难。考虑了这个对称性计算出的结果与实验严重不符;反而是忽略了这个对称性的简单估计给出了更接近实验的结果。这样的奇特情况暗示着应当存在一个理论上的机制,使得这个理应被保留的 $U(1)\times U(1)$ 对称性发生了一个破坏。进一步的理论研究展示了,这种破坏正是由于我们将一个无限自由度的经典理论进行了量子化导致的。
测度变换与手征反常
最直观地体现出反常与量子化关系的方法应当就是由 Fujikawa 给出的基于路径积分测度变换的计算。本小节我们来探讨在这种方法下对手征反常(也是 QCD 中最重要的反常)的计算。
首先写下一个与某种规范场有非手征耦合的无质量自旋 $1/2$ 费米子的路径积分:
\[\mathcal{Z}=\int[\mathscr{D}\psi\mathscr{D}\bar{\psi}\mathscr{D}A]\mathrm{e}^{-\mathrm{i}S}\]虽然我们目前讨论的手征反常是整体的,但从一些(稍后可以看到的,出于给出 Noether 定理的需求导致的)技术上的原因,我们考虑对费米场们做一个任意的定域幺正变换,即 $\psi(x)\rightarrow U(x)\psi(x)$. 基本的 Grassmann 代数规则告诉我们,在这样的变换下,泛函测度的变换为2:
其中我们有:
\[\begin{aligned} \mathscr{U}_{xn,ym}&=U(x)_{nm}\delta^4(x-y) \\\mathscr{\bar{U}}_{xn,ym}&=[\gamma^0 U(x)^{\dagger}\gamma^0]_{nm}\delta^4(x-y) \end{aligned}\]如果 $U(x)$ 是非手征的,即 $U(x)=\exp\{\mathrm{i}\alpha(x)t\}$,那么显然有 $\mathscr{U}\bar{\mathscr{U}}=1$,这意味着变换给出的行列式没有产生额外的贡献。但是如果 $U(x)$ 是手征的,即有 $U(x)=\exp\{\mathrm{i}\gamma_5\alpha(x)t\}$,那么事情就会出现问题。由于手性矩阵 $\gamma_5$ 与其余所有 gamma 矩阵的反对易性质,我们实际上有 $\mathscr{U}=\mathscr{\bar{U}}$,即 $\mathscr{U}$ 是赝“幺正”的。这导致测度变换带来的行列式项没有成对消去,反而变为了:
为了给出这个贡献的一个定量表达式,我们考虑该手征变换是无穷小定域变换的情况。利用 $\det=\exp\text{tr}\ln$ 的公式,我们可以得到:
\[(\det\mathscr{U})^{-2}=\exp\left\{\mathrm{i}\int\mathrm{d}^4x\:\alpha(x)\mathscr{A}(x)\right\}\]其中我们有:
\[\mathscr{A}(x)=-2\text{tr}\{\gamma_5 t\}\delta^4(x-x)\]显然这个 $\mathscr{A}(x)$ 包含一个类似 $0\cdot\infty$ 的情形,需要进行正规化计算。我们在这里不展示细节的正规化计算过程,大致的思路就是将 $\delta^4(0)$ 写成动量积分,再引入一个正规化因子分离发散,可以发现发散会被求迹抵消,剩下一个有限大的值。这里对正规化因子的引入要求保规范不变性,因而会同步引入那个与费米子耦合的规范场,进而带来最终的反常项。
最终的计算结果为:
\[\mathscr{A}(x)=-\frac{1}{16\pi^2}F_{\mu\nu}(x)\tilde{F}^{\mu\nu}(x)\text{tr}\{t_{\alpha}t_{\beta}t\}\]其中 $t_{\alpha}$ 是最初我们假定的理论中与费米子耦合的规范场所取值的李代数生成元。
现在我们显然地看到了场的积分测度确实会出现在对称变换下发生额外变化的情况,这已经展示出了对经典对称性的破坏。但是,作为一个物理上的对应,我们可以进一步展示一下这个破坏对 Noether 流带来的影响。考察对费米场做上述无限小手征变换所导致的 $\mathcal{Z}$ 的变化,有:
\[\begin{aligned} \delta\mathcal{Z}&=\int\delta\{[\mathscr{D}\psi\mathscr{D}\bar{\psi}]\}\mathrm{e}^{\mathrm{i}S}+[\mathscr{D}\psi\mathscr{D}\bar{\psi}]\delta\mathrm{e}^{\mathrm{i}S} \\&=\int[\mathscr{D}\psi\mathscr{D}\bar{\psi}]\left[\mathscr{A}(x)\alpha(x)+J_5^\mu(x)\partial_{\mu}\alpha(x)\right]\mathrm{e}^{\mathrm{i}S} \end{aligned}\]由于上式的变换仅仅是对积分变量做出的替换,而这实际上不会改变路径积分的值,因此 $\delta\mathcal{Z}=0$. 以往的情况下,这个条件应当给出 Ward 恒等式(或者其类似物),但在现今的情形下,我们发现这给出:
\[\langle\partial_\mu J^{\mu}_5(x)\rangle=\mathscr{A}(x)\]即流守恒方程不再成立,这明显地意味着轴矢量 $U(1)$ 对称性被破坏了。因此,我们需要对量子情形下的流守恒做出修正。如果有不错的注意力,我们可以观察到 $\mathscr{A}(x)$ 实际上可以被写为一个全导数(其中我们使用了伴随表示的归一化条件,这给出了 $N$):
\[\mathscr{A}(x)=-\frac{N}{8\pi^2}\partial_\mu\varepsilon^{\mu\nu\rho\sigma}\left[A_{\gamma\nu}F^{\gamma}_{\rho\sigma}-\frac{2}{3}C_{\alpha\beta\gamma}A^{\alpha}_{\nu}A^{\beta}_{\rho}A^{\gamma}_{\sigma}\right]\](顺带,这个被求导的部分被称为 Chern-Pontryagin 密度。随着涉及到拓扑学的内容逐渐增多,Chern 的名字将会在后续内容中多次出现。)因此我们可以重新定义一个反常“守恒流”:
\[\partial_\mu(J_5^\mu+K^\mu)=0\]其中有:
\[K^\mu=\frac{N}{8\pi^2}\varepsilon^{\mu\nu\rho\sigma}\left[A_{\gamma\nu}F^{\gamma}_{\rho\sigma}-\frac{2}{3}C_{\alpha\beta\gamma}A^{\alpha}_{\nu}A^{\beta}_{\rho}A^{\gamma}_{\sigma}\right]\]这便是修正后的反常轴矢流方程。
三角圈图与一般情况的反常
通过使用 Fujikawa 的方法,我们计算出了手征反常的结果。但对于一些其他的,更一般的反常(例如,我们下一节要讨论的规范反常和引力反常),一个直接的微扰论计算将是更加方便的。在本小节中,我们就来讨论直接计算三角圈图来获得反常的一些信息。特别的,我们不会将计算进行到底(因为最后有一些烦人的 Feynman 积分),对圈图的一个初步分析就可以给出我们所需要的关键参数。
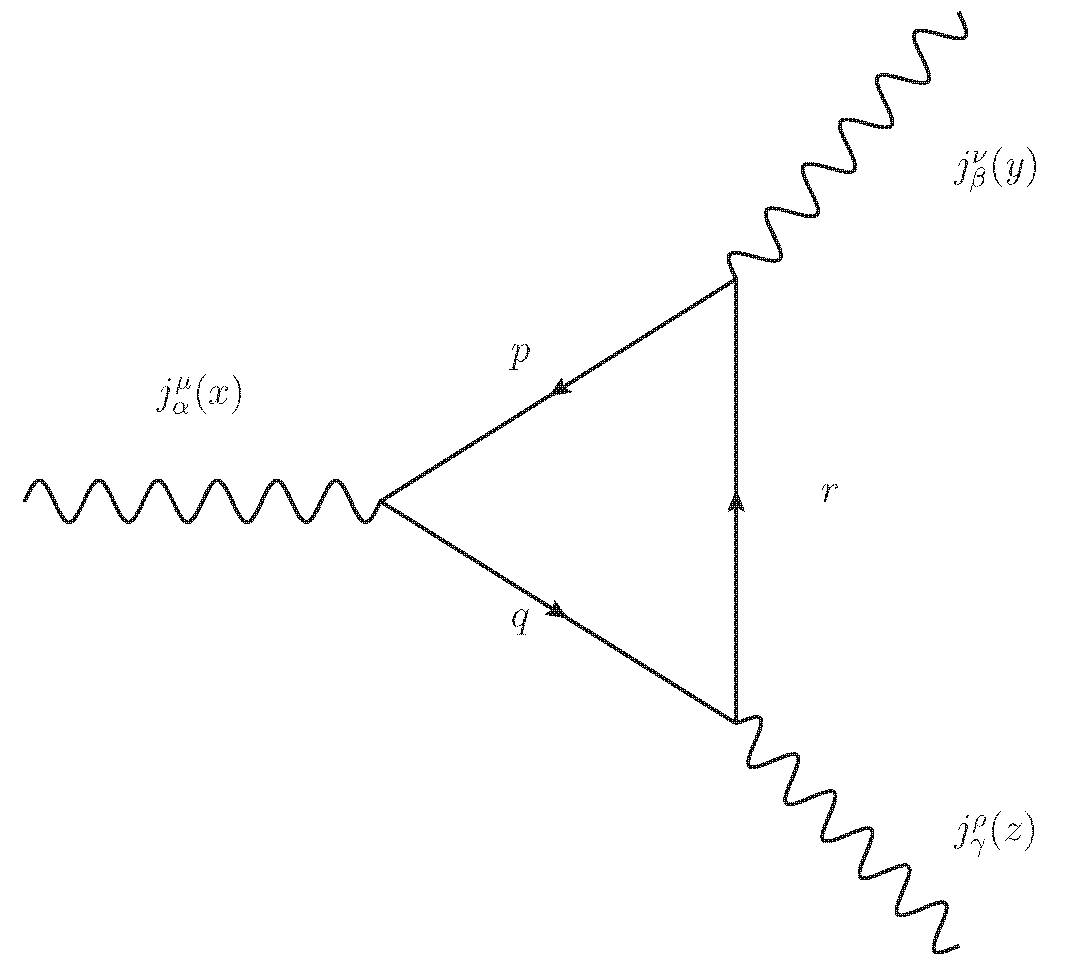
考虑一个与规范场有手征耦合的无质量费米子理论,在一圈阶会有一个如上图所示的圈图,以及一个交换 $j^\nu_\beta(y)$ 和 $j^{\rho}_\gamma(z)$ 的另一张图。这两张图给出了关联函数:
按费曼规则读图写下关联函数,这给出:
\[\begin{aligned} \Gamma^{\mu\nu\rho}_{\alpha\beta\gamma}(x,y,z)=&-\mathrm{i}\:\mathrm{tr}\left[S(x-y)\gamma^{\nu}T_{\beta}P_LS(y-z)\gamma^{\rho}T_{\gamma}P_LS(z-x)\gamma^{\mu}T_{\alpha}P_L\right] \\&-\mathrm{i}\:\mathrm{tr}\left[S(x-z)\gamma^{\rho}T_{\gamma}P_LS(z-y)\gamma^{\nu}T_{\beta}P_LS(y-x)\gamma^{\mu}T_{\alpha}P_L\right] \end{aligned}\]其中 $\mathrm{tr}$ 自动对所有旋量和规范指标求迹。
将传播子的表达式带进去并进行一些化简,我们会发现这个顶点对应的两张图的贡献分别正比于如下两个规范生成元乘积的迹:
\[\mathrm{tr}[T_{\beta}T_{\gamma}T_{\alpha}],\:\mathrm{tr}[T_{\gamma}T_{\beta}T_{\alpha}]\]为了后续的分析,我们可以将这个迹分为对称和反对称两部分:
\[\mathrm{tr}[T_{\beta}T_{\gamma}T_{\alpha}]=\mathrm{tr}\left[\frac{1}{2}\{T_{\alpha},T_{\beta}\}T_{\gamma}+\frac{1}{2}[T_\alpha,T_{\beta}]T_{\gamma}\right]=D_{\alpha\beta\gamma}+\frac{1}{2}\mathrm{i}NC_{\alpha\beta\gamma}\]其中我们使用了一个假定的归一化条件 $\mathrm{tr}[T_{\alpha}T_{\beta}]=N\delta_{\alpha\beta}$,并且 $C_{\alpha\beta\gamma}$ 是相应李代数的结构常数。我们注意到,被定义成加和中第一项的 $D_{\alpha\beta\gamma}$ 关于 $\alpha\beta$ 是对称的,第二项则是反对称的。
接下来我们考察 Ward 恒等式。如果这三个流都是守恒的,那么 Ward 恒等式会告诉我们:
\[\frac{\partial}{\partial x^{\mu}}\Gamma^{\mu\nu\rho}_{\alpha\beta\gamma}(x,y,z)=-\mathrm{i}C_{\alpha\beta\lambda}\delta^4(x-y)\langle \mathrm{T}\{j^{\nu}_{\lambda}(y)j^{\rho}_{\gamma}(z)\}\rangle-(\gamma\rightarrow\beta\rightarrow\lambda)\:\text{term}\]这其中只有关于 $\alpha\beta$ 的反对称项,而不存在正比于 $D_{\alpha\beta\gamma}$ 的对称项!因此这个对称项的存在正代表了理论中对称性被破坏的贡献,也就是我们所面临的反常。
这张三角圈图可以被进一步计算下去,利用平移被积分动量的方式进行正规化。这个结果不是本文讨论的重点,因而我们简单介绍一下过程。由于我们有两个被积动量,这里的平移变量有至少两个选取上的自由度,对应于一些选择的技巧。我们希望能够将这张图的反常都集中在一个流上,因此我们会额外对另两个流附加 Ward 恒等式的限制。这给可能的选取做出了一个限制。在这个限制下,进一步的计算确切保证了任何选取的方法都不能把正比于 $D_{\alpha\beta\gamma}$ 的反常项彻底的消去,因此只要这个对称迹张量不为零,三角圈图就确实会给出一个非零的反常贡献。
规范反常、引力反常与理论的自洽性
在上一小节中,我们通过计算圈图的方式看到了反常贡献的存在性被对称张量 $D_{\alpha\beta\gamma}$ 所决定。对于整体对称性,反常的存在没有什么很大的问题,其充其量只是改变了理论的一些经典预言结果。然而,如果反常发生在一个规范对称性上,那么这将是灾难性的。规范对称性出现反常意味着理论的 Lorentz 不变性会遭到破坏,BRST 对称性与相应的可重整性也会出现问题,这些都会导致理论出现不自洽性。因此,我们需要有能力考察一个理论是否能够保证其在规范对称性上不出现反常。
理论不出现反常对应两种可能性,一种是对于相应的规范耦合,$D_{\alpha\beta\gamma}$ 为零,这意味着反常直接不存在于这种规范对称性中。另一种可能则是理论中所有粒子给出的反常贡献中,所有的 $D_{\alpha\beta\gamma}$ 相互抵消,总和为零,这保证了理论在总体层面上实现了没有反常。
除了规范反常之外,引力反常也是理论要考虑的问题。虽然现有的可重整理论没有将引力包含进来,但仍旧不妨碍我们将引力作为有效理论引入到模型当中。当三角圈图的两条外流被引力流替代时,我们需要保证在背景引力场下理论不会出现反常带来的自洽性问题。
在考虑到反常的自洽性问题后,一个自然的问题是:现有的标准模型是否能够保证自洽无反常?本小节我们便来讨论这个话题。
我们知道,李代数的表示可以被分为实(赝实)和复两类,其被是否满足如下关系区分:
\[(\mathrm{i}T_{\alpha})^*=S(\mathrm{i}T_{\alpha})S^{-1}\]如果代数的表示满足上式,即其复共轭与原始表示等价,那么我们就称这种表示是实(或赝实)的。一般生成元被我们取成厄米的,因此上述条件同样可以被写为:
\[T_{\alpha}^{\top}=-ST_{\alpha}S^{-1}\]将这个条件带入 $D_{\alpha\beta\gamma}$ 的表达式,我们发现:对所有实(赝实)表示,总有:
这意味着,对所有的实(赝实)表示,我们的理论没有反常。
接下来我们考虑标准模型 $\text{SU}(3)\times\text{SU}(2)\times\text{U}(1)$ 规范理论。$D_{\alpha\beta\gamma}$ 表达式中的三个生成元对应于三角圈图三个顶点的规范场。为了探讨规范反常的抵消,我们需要考虑所有这些生成元的可能取法。所有包含单个 $\text{SU}(2)$ 和 $\text{SU}(3)$ 的取法都会使得 $D_{\alpha\beta\gamma}$ 包含一个单独的 $\text{tr}[T_{\alpha}]$ 项,而这一项对 $\text{SU}(2)$ 和 $\text{SU}(3)$ 这样的单 Lie 代数来说都是零,进而使得 $D_{\alpha\beta\gamma}$ 也是零,因而我们不用考虑它们。由于 $\text{SU}(2)$ 的表示总是实或赝实的,因此三个 $\text{SU}(2)$ 的可能性也不需要考虑进来。于是我们可以给出以下四种可能的生成元取法:$\text{SU}(3)-\text{SU}(3)-\text{SU}(3)$, $\text{SU}(3)-\text{SU}(3)-\text{U}(1)$, $\text{SU}(2)-\text{SU}(2)-\text{U}(1)$, $\text{U}(1)-\text{U}(1)-\text{U}(1)$. 当我们在一代费米子中考虑这些反常条件并要求它们相消的时候,三个 $\text{SU}(3)$ 的情形由于所有一代费米子的表示共同构成了一个实表示,其没有额外的反常贡献。而对于剩余的取法我们会发现这给出了关于 $\text{U}(1)$ 超荷数值的一个限制。列出所有的一代费米子所属的规范群表示:
| 粒子 | $SU(3)_C$ |
$SU(2)_L$ |
$U(1)_Y$ 超荷 |
|---|---|---|---|
$q_L$ |
$\mathbf{3}$ | $\mathbf{2}$ | $a$ |
$u_R^c$ |
$\bar{\mathbf{3}}$ | $\mathbf{1}$ | $b$ |
$d_R^c$ |
$\bar{\mathbf{3}}$ | $\mathbf{1}$ | $c$ |
$\ell_L$ |
$\mathbf{1}$ | $\mathbf{2}$ | $d$ |
$e_R^c$ |
$\mathbf{1}$ | $\mathbf{1}$ | $e$ |
上述剩余的三个取法给出了如下的限制:
$\text{SU}(3)-\text{SU}(3)-\text{U}(1)$:
\[2a+b+c=0\]$\text{SU}(2)-\text{SU}(2)-\text{U}(1)$:
\[3a+d=0\]$\text{U}(1)-\text{U}(1)-\text{U}(1)$:
\[2\times 3a^3+3b^3+3c^3+2d^3+e^3=0\]除此之外,我们还需要考虑一个情形:在三角图的两个背景流为引力的情况下,理论不能出现反常。容易猜到,引力流直接和费米子以能动张量形式耦合,因此它没有对应的生成元项,于是引力反常直接正比于 $\text{tr}[T_{\alpha}]$,所以我们只需要考虑引力-引力-$\text{U}(1)$ 的情况:
引力-引力-$\text{U}(1)$:
\[2\times 3a+3b+3c+2d+e=0\]求解这四个方程,我们会发现其只能给出两组解,其一为:
\[b=-4a,c=2a,d=-3a,e=6a;\]另一组则为:
\[b=-c,a=d=e=0.\]第一组解正好(在相差一个归一化常数下)是实验所观测到的 $\text{U}(1)$ 超荷的值,其与各粒子所带电荷相符合;而第二组解则与任何实验观测结果不符。这个结果告诉我们,基本粒子的超荷值(进一步的,电荷值)是被规范反常相消的自洽性条件限制住的。